
el esc
é
ptico
50
Invierno 2018/19
Introducción
Hasta hace un par de años, cuando pensábamos
en niños sin vacunar, casi sin querer nos imaginába-
mos un niño africano, o algún miembro de un pueblo
aislado en mitad de la selva o las montañas. Quizás
teníamos algún amigo que no había vacunado a sus
hijos, y que supuestamente lo había hecho de mane-
ra informada, asegurándose (decía) de que esa deci-
sión era la mejor. Pero en cuestión de pocos meses
empezamos a leer noticias relacionadas con muertes
por sarampión (¡Sarampión! pero si de pequeños lo
pasábamos muchos…y morían algunos): un niño ita-
liano con leucemia que había sido contagiado por sus
hermanos no vacunados
1
; o más recientemente la jo-
ven francesa que no podía ser vacunada debido a su
inmunodepresión
2
. Hay más: un brote que se originó
en Disneylandia (California) y que en cuestión de un
mes se había extendido a 125 casos repartidos en ocho
Estados, correspondiendo más de la mitad de ellos a
personas sin vacunar, casi todas por elección
3
.
En muchas de estas noticias, además, se habla de
un mágico umbral del «95%», que no se puede cruzar
hacia abajo sin que haya peligro de propagación del
sarampión, afirman.
Comenzamos a
googlear
y encontramos que el sa-
rampión está volviendo al primer mundo en general,
y a Europa en particular, de manera alarmante (hemos
pasado de 1346 casos en 2008 a 19 570 en 2017 y la
situación es crítica en varios países
4
; Véase Fig. 1);
descubrimos el movimiento antivacunas, que en las
redes es bastante activo y puede dar la falsa sensación
de tener gran número de seguidores; descubrimos el
esfuerzo de médicos e investigadores (hay otro
cien-
tíficos
aquí al lado) que, con argumentos científicos
y números en la mano, defienden la necesidad de la
vacunación (aunque ellos son menos visibles en la
red).
5
-
6
Vamos a intentar contestar dos preguntas, siempre
desde nuestro punto de vista matemático: 1) ¿Por qué
algunas personas del primer mundo han decidido no
vacunar(se)? ¿Es tan numeroso como ruidoso el mo
-
vimiento antivacunas?; y 2), ¿pueden decirnos las ma
-
temáticas cómo erradicar los casos de sarampión del
mapa y por qué ese 92-95% de vacunados parece dar
un 100% de seguridad?
Vamos a centrarnos en Europa, donde hay suficien
-
tes vacunas de sarampión para todos y donde, además,
son gratuitas. Aunque antes de seguir debemos decir
que cuando estábamos pensando sobre esto, leímos un
libro delicioso que nos sirvió como guía y que quere-
mos recomendar desde ya a cualquier persona intere-
sada en profundizar más en este tema
7
.
¿Por qué algunas personas han decidido no va-
cunarse o no vacunar a sus hijos?
Tenemos a nuestro bebé sano en nuestros brazos,
queremos lo mejor para él, y lo mejor es que ese niño
siga lo más sano posible. Es decir, queremos tomar las
decisiones que minimicen el riesgo de que a ese bebé
le pase algo malo.
La vacuna
solidaria
Ana Granados y Ana Portilla, Dept. Matemáticas, Saint Louis University, Madrid
Campus.
Las matemáticas demuestran la solidaridad de las vacunas, porque 93 = 100%
D
ossier
el esc
é
ptico
51
Invierno 2018/19
Vamos a plantearnos este problema desde el punto
de vista de la teoría de juegos, donde los jugadores (en
este caso los padres) somos seres
racionales
que to-
mamos las
mejores decisiones
a partir de la
informa-
ción
que tenemos en ese momento. ¿Cómo podemos
perder en este juego? Pues perdemos bien si nuestro
bebé se contagia de la enfermedad para la que no le
hemos vacunado, bien si la vacuna que le hemos pues-
to le provoca efectos secundarios. Queremos minimi-
zar la pérdida del juego. Si traducimos esta situación
en una ecuación, que a los matemáticos es lo primero
que nos sale, diríamos algo así:
Pérdida = riesgo con-
tagio + riesgo efectos secundarios
. O para ponerlo
más matemático aún,
P = RC + RES
La pregunta real es cómo de grande es cada su-
mando. Cuando nos paramos a pensarlo y miramos a
nuestro alrededor, normalmente no conocemos a tan-
tos niños que en los últimos años hayan enfermado
de sarampión (incluso la mayor parte de nosotros no
conocerá a ninguno… porque las vacunas cumplen su
misión). Así que, la ecuación anterior ya se ha con-
vertido en
P =
RC
+ RES
Y parece obvio que la mejor decisión para la salud
de nuestro hijo es no vacunarlo. Si además en junio
del 2017 fuimos uno del millón de oyentes que escu-
chó el programa de radio «Levántate y Cárdenas», de
Javier Cárdenas
8
, o uno de los más de diez millones
que vio a Donald Trump en el tercer debate durante
las elecciones primarias del Partido Republicano en
septiembre del 2015
9
-
10
,
habremos sido informados
de
que la vacuna del sarampión puede provocar autismo.
Si ante la duda suscitada buscamos por la red, vere-
mos que una investigación del médico inglés Andrew
Wakefield publicada en 1999 por la prestigiosa revista
The Lancet
prueba esta afirmación
11
. Entonces, la lec-
tura de la ecuación se parecerá más a algo como
P =
RC
+
RES
!!!!
Y no vacunar a nuestro bebé sano parecerá no sólo
la mejor decisión, sino casi la única sensata.
¿Por qué RES parece grande o por qué si te ca-
sas en Kentucky matas a un pescador?
La historia del fraude de Wakefield, que proclamó
haber descubierto una conexión entre la vacuna triple
vírica (sarampión, paperas y rubeola) y el desarrollo
de autismo es bien conocida y está muy bien docu-
mentada
12
-
13
. De hecho, la historia termina como el
rosario de la aurora:
The Lancet
tiene que retirar el
artículo por carecer de base científica y Wakefield es
expulsado de la medicina en Inglaterra y acusado por
el Consejo General de Medicina del Reino Unido de,
entre otras cosas, haber sometido a niños con proble-
mas de desarrollo infantil a pruebas agresivas innece-
sarias.
El autor del artículo periodístico donde se desta-
pó este fraude, Brian Deer, publicó un libro sobre su
investigación
14
.
Se supieron algunas cosas muy feas,
como que en 7 de los 12 casos estudiados los trastor-

el esc
é
ptico
52
Invierno 2018/19
nos habían aparecido
antes
de que los niños hubieran
sido vacunados, y no después; o que un estudio de
abogados había pagado a Wakefield para crear prue
-
bas e iniciar una demanda contra las compañías que
fabricaban la vacuna
.
El ex doctor Wakefield sigue
muy activo en el movimiento antivacunas de Estados
Unidos. De hecho, y junto a otros tres prominentes
miembros de este movimiento, se reunió con Donald
Trump en un acto para recaudar fondos para el Parti-
do Republicano, meses antes de las declaraciones del
candidato durante el debate de las primarias de dicho
partido.
15
Una investigación desarrollada en EE.UU. demos-
tró rotundamente hace dos años que la vacuna del sa-
rampión, las paperas y la rubéola no es la responsable
de los casos autismo. Se trata de las conclusiones de
un estudio realizado en más de 95 000 niños nortea-
mericanos y que confirmó
que dichas vacunas no
se asocian a un mayor riesgo de trastorno del
espectro autista
, ni siquiera en aquellos menores
cuyos hermanos sufren esta patología.
16
Volvamos a las matemáticas para intentar entender
por qué el sumando RES está tan magnificado por el
movimiento antivacunas y por qué se difunde más el
bulo de que la vacuna produce autismo que la infor-
mación real que lo desmiente.
Para empezar, la conexión vacuna-autismo no pa-
rece tan descabellada: es común que conozcamos a
alguien que tenga un trastorno del espectro autista (la
incidencia del TEA se estima en 1 de cada 100 naci-
mientos), y casi con seguridad le fue diagnosticado
durante el segundo o tercer año de vida
17
. En la ma-
yoría de los países europeos y en Estados Unidos, la
vacuna triple vírica se administra durante este mismo
periodo
18
,
así que si hacemos un gráfico mental entre
la edad en la que los niños
desarrollaron
autismo y
aquella a la que fueron vacunados, posiblemente nos
salga una correlación altísima. Y entonces es fácil que
caigamos en la trampa de pensar que, si están
correla-
cionados
, es porque una debe
causar
la otra.
Si comparamos el número de gente que se ahoga
tras caerse de un barquito de pesca con el número de
matrimonios en el estado de Kentucky, veremos que
están altamente correlacionados
19
(¡con un índice del
95%!, una barbaridad en matemáticas). Sin embargo,
y para tranquilidad de los kentuckianos que estén pen-
sando en el matrimonio,
es obvio que el hecho de que
sean más propensos a pasar por la vicaría no provoca,
de ninguna manera, que se ahoguen más pescadores.
Es decir,
correlación no implica causalidad
. Inclu-
so aunque la edad de detección del TEA y la de vacu-
nación estuvieran altamente correlacionadas, una no
tendría por qué ser causa de la otra, y eso es justamen-
te lo que ocurre, como todos los trabajos científicos
realizados hasta el momento afirman.
En esta época del
Big Data
, no es difícil establecer
correlaciones entre situaciones bien dispares. A veces
estas correlaciones tienen una finalidad simpática,
como las que propone Tyler Vigen. Pero otras veces,
la finalidad puede ser algo más siniestra, como cuan
-
do nos presentan datos (o no, a veces una afirmación
sin más vale
20
) de aumento de inmigración en una
zona correlacionados con datos de aumento de peli-
grosidad, e intentan producir la conclusión falaz de
que el segundo seguro es causa del primero, a pesar
de muchos estudios que evidencian la falsedad de esta
relación
21
-
22
.
Vale, no existe relación alguna, pero muchos de
nosotros hemos oído este argumento, el movimiento
antivacunas parece seguir creciendo, y el número de
personas que decide no vacunar a sus hijos del sa-
rampión parece ir en aumento, tal y como muestra el
mapa del comienzo. ¿Nos dicen algo las matemáticas
al respecto?
Pensemos en algunos nombres asociados al movi-
miento antivacunas que defienden que la triple vírica
produce autismo: Jim Carrey, Jenny McCarthy, Alicia
Silverstone, congresistas norteamericanos como Dan
Burton, además de los ya mencionados Trump y Cár-
denas. Se trata de personas muy famosas, con capaci-
dad para hacerse oír en distintos foros (no solamente
en canales dedicados a hablar de vacunas o autismo)
El movimiento antivacunas es bastante activo en las redes
y puede dar la falsa sensación de tener gran número de se-
guidores.
el esc
é
ptico
53
Invierno 2018/19
y expresar sus ideas. Son
influencers
del movimiento,
por así decirlo. El caso concreto de Trump fue des-
mentido por expertos en TEA
23
, pero no tuvo tanta
repercusión.
No solo eso. Antes, cuando queríamos información
sobre salud (u otras cosas), preguntábamos al médi-
co. Ahora, y cada vez con mayor frecuencia, también
buscaremos en internet. Un estudio
24
introdujo los tér-
minos «
vaccination
» e «
immunisation
» en Google y
observó que los primeros diez resultados devolvieron
páginas antivacunas (vamos, estupendo). Un análisis
de vídeos de YouTube sobre vacunación encontró que
el 32% se oponía a ella y que estaban mejor clasifi
-
cados y tenían un mayor número de visitas que los
provacuna
25
; el 43% de blogs en MySpace sobre va-
cunación la evaluaba de manera negativa, y refería a
organizaciones críticas con las vacunas que, además,
contenían información incorrecta.
El hecho de que la mayoría de la población siga
vacunada indica que los antivacunas son muy pocos,
pero tienen mucha voz, y pueden hacernos pensar a
los demás que sus
creencias son mayoritarias
cuando
están bien lejos de serlo. Estamos ante lo que se co-
noce como
el espejismo
de la mayoría
26
, y queda muy
bien explicado en el siguiente ejemplo
27
:
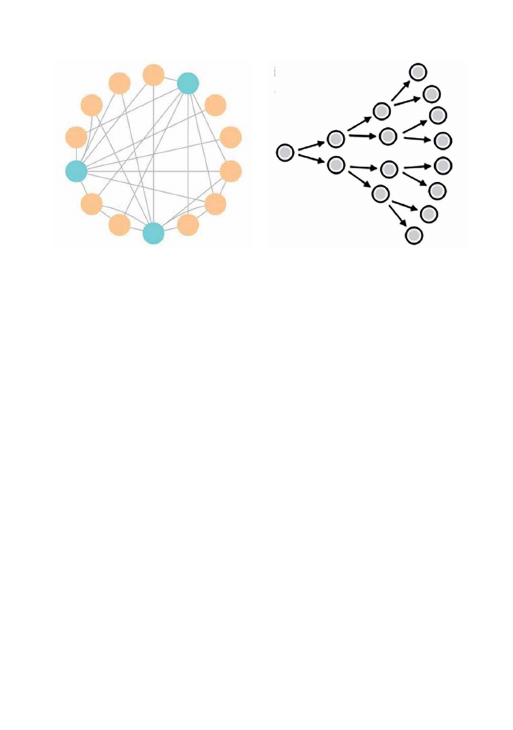
En la Figura 2 modelizamos una red de relaciones,
por ejemplo, de un pequeño pueblo. Cada círculo re-
presenta una persona, y dos personas que se conocen
están unidas por una línea. Los círculos azules sim-
bolizan personas que piensan que la vacuna del sa-
rampión produce autismo (
causalistas
, para abreviar);
los círculos naranjas, a personas que no opinan así. Si
un individuo se pregunta cuántos
causalistas
hay, lo
razonable es que mire primero si sus amigos lo son.
En el ejemplo concreto del pueblo de nuestro gráfico,
se puede observar que la mayoría de los habitantes va
a pensar que hay muchos, si únicamente se basa en
su red de amistades para responder a esta pregunta.
Pero esto es algo chocante, porque nosotros estamos
viendo que, de hecho, la mayoría de los círculos son
naranjas, es decir,
no causalistas.
La razón que expli-
ca este hecho es que los azules son
influencers
, es de-
cir, individuos muy populares conocidos por todos los
naranjas. La opinión de una minoría termina dando
voz a la mayoría, y en algunas redes, la información
sesgada a la que accedemos puede llevarnos a la con-
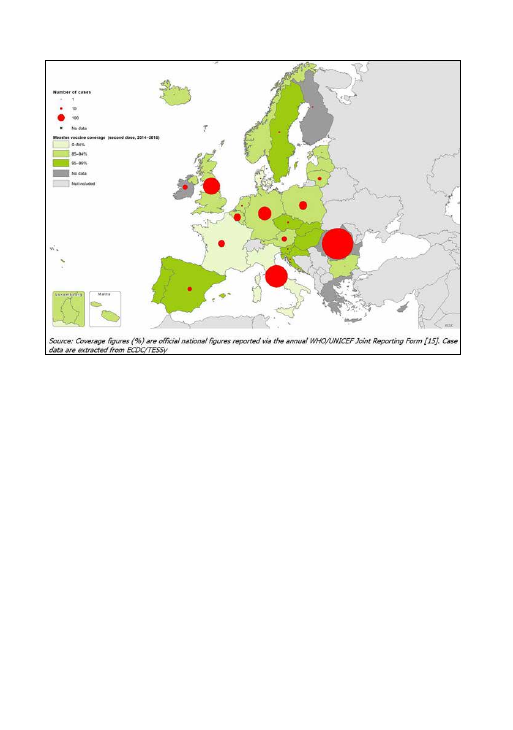
Fig. 1. Número de casos de sarampión en la UE entre el 1 de febrero de 2016 y el 31 de enero de 2017 (puntos rojos) y % de población vacunada (en tonos
de verde). Figura: European Center for Disease Prevention and Control, pág. 2., https://ecdc.europa.eu/sites/portal/files/media/en/publications/Publications/27-
02-2017-RRA-Measles-Romania,%20European%20Union%20countries.pdf
el esc
é
ptico
54
Invierno 2018/19
clusión errónea. En las redes sociales, la mayoría de
las páginas están conectadas con páginas de opiniones
similares, y las páginas más visitadas son también las
más sugeridas. Por tanto, es posible pensar que nues-
tro pequeño pueblo del ejemplo anterior modeliza, en
cierto sentido, las relaciones que se establecen en in-
ternet.
Mirando el tamaño de RC (Riesgo de Contagio)
con las gafas correctas
Cuando al mirar la fórmula vemos un RC tan pe-
queñito, es porque estamos siendo víctimas de la
ra-
cionalidad miope
. Es decir, obviamos el hecho de que
la mayor parte de la gente de nuestro entorno está va-
cunada, y justamente por ello percibimos el RC de la
ecuación así de pequeño. Si, basándonos en eso, todos
tomáramos la decisión de no vacunar, comenzaría a
haber mucha gente en nuestro entorno susceptible de
contraer el virus y el riesgo de ser contagiados por uno
de los infectados aumentaría. Es posible incluso que
el tamaño de ese primer sumando no solo volviera al
que le corresponde de verdad en la ecuación inicial,
sino que se podría incluso hacer subjetivamente mu-
cho más grande. Esto es lo que el mapa que hemos
visto al principio parece sugerir, y esto es lo que las
matemáticas van a demostrar.
Para contestar a la pregunta de qué puede pasar si
dejamos de vacunarnos, lo único que tenemos que ha-
cer es predecir el futuro. Es decir, utilizar lo que ya
sabemos para pronosticar la respuesta. Esto es justa-
mente lo que hace un buen modelo matemático
28
.
Cada mañana laboral tenemos que elegir la ropa
que nos pondremos. Para ello, cada uno tiene en cuen-
ta la información que ha acumulado hasta el momento
(qué tipo de ropa hay en el armario, si va a desplazarse
en transporte público o privado, si se experimentan
grandes diferencias de temperatura entre el transporte
y la calle, etc.); decide qué variables va a priorizar
(se puede valorar mucho la comodidad y no dar tanta
importancia a la diferencia de temperatura, por ejem-
plo). Además, también puede tener en cuenta otras
cosas a la hora de decidir qué ropa ponerse, como si
hoy habrá una reunión importante o si a la salida del
Las vacunas no se asocian a un mayor riesgo de trastorno
del espectro autista, ni siquiera en aquellos menores cuyos
hermanos sufren esta patología.
Fig. 2. Modelización de una red de relaciones entre habitantes de un
pequeño pueblo.
Fig. 3. Representación de la expansión de un hecho que sigue una función
exponencial 2
m
.

el esc
é
ptico
55
Invierno 2018/19
trabajo irá al gimnasio. Este es el modelo informal de
cada uno, y está ajustado a nuestra experiencia pasada
y los datos que tenemos. No le valdría, por ejemplo, a
nuestro sobrino de cinco años. Además, cada día eva-
luamos el éxito de la elección de vestuario en función
de lo cómodos que nos hemos encontrado o de cuánto
frío hemos pasado, y esto permite ajustar y mejorar
el modelo. Seguramente, tras más de veinte años con
mañanas laborales, tendremos el modelo bastante per-
feccionado.
Un modelo matemático es un proceso que usa ma-
temáticas para representar, analizar y hacer prediccio-
nes sobre fenómenos del mundo real. Como en todo
modelo científico, observamos lo que ocurre en la
realidad, recogemos datos, encontramos relaciones
entre ellos, traducimos esas relaciones a ecuaciones
matemáticas, predecimos lo que ocurrirá solucionan-
do esas ecuaciones, y finalmente validamos el modelo
comparando la realidad con los resultados predichos,
para poder ir ajustando el modelo hasta que el resulta-
do sea satisfactorio. Es un modelo científico, así que
cualquiera podrá reproducirlo.
Por ejemplo, en una fiesta que organiza nuestra hija
en casa, observamos que durante el primer minuto
hay 1 persona morena vestida de azul; en el segundo
minuto, 2 personas, una morena y otra pelirroja, ves-
tidas ambas de azul; en el tercer minuto, 6 personas,
3 morenas, 2 rubias y 1 pelirroja, todas vestidas de
azul; y el cuarto minuto, 8 personas, todas morenas
y todas vestidas de azul. Si estamos interesados en
saber si vamos a tener que pedirle a algún vecino que
nos deje trasladar la mitad de la fiesta a su casa, nos
interesa predecir el número de personas que habrá el
décimo minuto o el vigésimo; solo la información re-
lativa al número de personas es relevante, y en cam-
bio descartaremos el color de pelo o ropa. En estado
de pánico, notamos que el número de invitados varía
con el tiempo de manera que en el minuto
m
hay
2m
personas. En lenguaje matemático, nuestro modelo
propuesto es
N(m) = 2m
. Ahora observaríamos qué
ocurre durante los siguientes minutos y en el caso de
que esta relación se siga
casi siempre
diremos que el
modelo es válido y que, por tanto, en dos horas ha-
brá 120 invitados y, definitivamente, necesitaremos
varias casas vecinas. En otro caso, iremos ajustando
el modelo. Obviamente, cuanto más datos tenga para
validar mi modelo o más observaciones pueda hacer,
más fiable será.
Casi siempre, los fenómenos que observamos es-
tán en cambio continuo, y lo que medimos es justa-
mente ese cambio. Por ejemplo, si volvemos al caso
del sarampión, más que cuánta gente infectada hay
en un momento concreto, nos puede interesar
cómo
está cambiando
ese número de infectados, es decir,
si está aumentando o no (y a qué ritmo), pues esto
nos dará más información a la hora de valorar si, por
ejemplo, podemos estar ante un peligro de epidemia y
sabremos mejor cómo actuar. En matemáticas, la he-
Campaña de vacunación del HPV en colegios de Sao Paulo Brazil March 2014 (Foto: Pan American Health Organization PAHO)

el esc
é
ptico
56
Invierno 2018/19
rramienta que nos permite estudiar cómo cambia un
sistema es la conocida
derivada.
Un modelo de juguete y una poda de árboles
Si en lugar de una fiesta razonable como la de arri
-
ba hubiéramos organizado otra con la condición un
poco loca de que el primer minuto llegara un invita-
do, el segundo viniera un amigo del invitado que ya
estaba, el tercer minuto viniera un amigo nuevo por
cada invitado que ya estuviera, y así sucesivamente,
en 32 minutos tendríamos en casa a toda la población
mundial, y la amistad con los vecinos se habría per-
dido en el minuto 5 o 6, más o menos. Resulta que
lo que está pasando es que, cada minuto, el número
de invitados se va
doblando
. Mi modelo ahora sería
N(m) = 2
m
,
es decir, está representado por la conocida
función exponencial.
Pues así se comportaría nuestro sarampión, solo
que multiplicando por 18 cada vez en lugar de por 2.
Vamos a jugar un poco con un modelo muy simplifi
-
cado de cómo se propaga una enfermedad contagiosa,
así, como para andar por casa
29
.
Cada enfermedad tiene asociado un
número bá-
sico de reproducción
denotado por
R
0
, que estima
el número promedio de casos nuevos que genera un
caso dado a lo largo de un periodo infeccioso
30
. En
el caso de nuestra fiesta loca,
R
0
=2 ; en el caso del
sarampión,
R
0
varía entre 12 y 18.
Una manera muy visual de ver cómo está aumen-
tando el número de invitados en mi fiesta es usando
un arbolito como el de la figura 3. Cada nodo da lugar
a dos nuevas ramas y, como vemos, el árbol se hace
rápidamente muy frondoso.
Simplificando mucho las cosas, de cada nodo del
árbol del sarampión
brotarían 12 ramas en el me-
jor de los casos, y 18 en el peor (básicamente cier-
to, porque la probabilidad de contagio a personas no
protegidas es del 90%). Si quisiéramos evitar que el
número de ramas creciera descontroladamente, es de-
cir, si quisiéramos evitar que el sarampión se propa-
gara, de cada nodo deberíamos podar 11 en el primer
caso y 17 en el segundo (ya hemos visto que, aunque
dejásemos solo dos ramas, los números se irían de
madre y se infectaría toda la población del planeta
en un pispás). Claro, puestos a podar, ganas dan de
podar todas las ramas y terminar de manera radical
con el sarampión, ¿verdad? Sin embargo, aquí,
podar
equivale a vacunar y, desgraciadamente, no todo el
mundo puede ser vacunado (niños inmunodeprimi-
dos, personas con cáncer, embarazadas, etc.), así que
nuestro modelo debe también reflejar esta realidad y
para ello hay que dejar siempre una rama sin podar.
Así, este modelo tan de juguete nos dice que, para
tener controlado el sarampión, deberíamos vacunar
(inmunizar, podar) 11 de cada 12 ramas o 17 de cada
18, es decir, entre el 92% y el 95% de la población.
Es matemático:
la vacuna es solidaria
. Y esto es
válido para todas las enfermedades para las que existe
vacuna; el porcentaje de gente que necesita ser vacu-
nada para que
todos
estemos protegidos dependerá de
lo grande que sea
R
0
, pero siempre podemos calcular-
lo, y, por tanto, erradicar enfermedades contagiosas
para las que se disponga de vacuna. Este fenómeno se
conoce como
efecto rebaño
, y la idea que hay detrás
es que cuando llueve, si hay un número suficiente de
personas con sus paraguas abiertos, podremos cami-
nar sin mojarnos aunque nosotros no dispongamos de
uno. Pero como en alguna zona haya poca densidad
de paraguas, ahí, sin duda nos mojaremos.
Es verdad, todo esto lo estamos deduciendo de un
modelo de juguete. ¡Vamos con el de verdad!
Modelo SIR-v, o cómo las matemáticas demues-
tran la solidaridad de la vacuna
El modelo SIR se propuso por primera vez en
1927
31
,
y se ajusta muy bien a una enfermedad como
el sarampión. Antes de seguir, queremos volver a re-
ferir al lector al capítulo 5 de [8]
para una explicación
más detallada y muy clara de las matemáticas tras el
modelo.
Dividimos la población de un determinado lugar (o
de todo el mundo, da igual) en tres grupos: personas
susceptibles
de contagiarse de sarampión, personas
infectadas
y personas
recuperadas
(de ahí el imagi-
Un estudio introdujo los términos «
vaccination
» e «
immu-
nisation
» en Google y observó que los primeros diez resul-
tados devolvieron páginas antivacunas.
el esc
é
ptico
57
Invierno 2018/19
nativo nombre de SIR). Por
personas recuperadas
vamos a entender aquellas personas que ya han pa-
sado el sarampión y, o bien han salido de la enfer-
medad, o bien se han muerto (es una acepción algo
morbosa de la palabra
recuperado
, es cierto). Lo que
este modelo nos propone es algo bien razonable, y
hace hincapié en cómo la población de estos tres gru-
pos cambia con el tiempo (es decir, estamos hablando
de derivadas). El número de recuperados aumentará
solo con el de infectados; por otro lado, cada vez que
un susceptible y un enfermo se encuentren, el prime-
ro podrá contagiarse, así que estos encuentros hacen
que la población de susceptibles crezca; finalmente,
la población de infectados aumentará tanto como la
de susceptibles disminuya, y disminuirá tanto como
aumente el grupo de recuperados.
Si traducimos este párrafo a lenguaje matemático y
hacemos unos cuantos cálculos, estos nos dicen que
la única forma que tenemos para controlar el aumento
en el número de infectados (vamos, de controlar una
epidemia) es reducir al máximo el número de per-
sonas susceptibles
antes de que llegue el virus.
No
existe otra forma. Y la única manera de conseguirlo
es vacunando.
Y, además, al igual que hacíamos en el modelo de
juguete con la poda de árboles, en este modelo de ver-
dad, muy ajustado al sarampión, podemos cuantificar
qué porcentaje
tenemos que vacunar: al menos
R
0
-1
R
0
¡justo lo que nos decía nuestro modelo de juguete!
Cómo conseguir que 95% = 100%. Y matemáti-
camente probado
Como una imagen vale más que mil palabras, ilus-
tramos los resultados que predice el modelo expuesto
arriba con cuatro gráficos
32
(FIG. 4). Vamos a con-
siderar una población de 100 000 habitantes, donde
al principio no hay más que un infectado. En cada
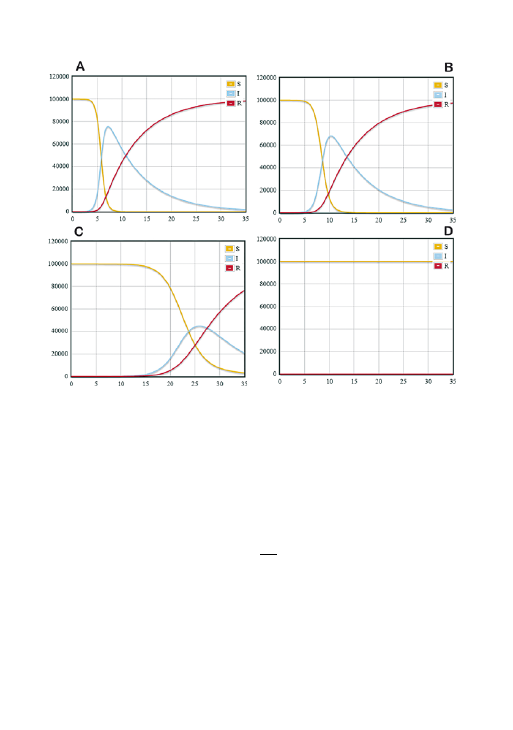
Fig. 4. Resultados del modelo para porcentajes de vacunación del 0% (A), 30% (B), 70% (C) y 93% (D), en una población de 100 000 personas.
S: Personas susceptibles; I: Personas infectadas; R: Personas recuperadas.

el esc
é
ptico
58
Invierno 2018/19
gráfico vemos tres curvas, y cada una de ellas va a
representar la población de susceptibles, infectados y
recuperados según van pasando los días. Lo que dife-
rencia un gráfico de otro es el porcentaje de población
vacunada al principio: 0%; 30%; 70% y 93% respec-
tivamente.
Es interesante observar cómo no solo el máximo
número de infectados (el
pico
de la gráfica azul) va
siendo más bajo según aumenta el porcentaje de va-
cunados, sino que además tarda más tiempo en pro-
ducirse (con lo cual permite una reacción mayor ante
epidemia) y que en el último gráfico no hay infectado
alguno. Con una tasa de vacunación del 93%,
todos
estamos protegidos
, incluso ese 7% que no se vacunó.
Conclusión
El modelo SIR-v lleva años de datos recogidos,
mejoras, ajustes, y validaciones con resultados de va-
cunaciones sistemáticas de población
33
. Vamos, que
es un buen modelo, nos podemos fiar de él.
Los gráficos de la Figura 4
nos ilustran qué ocurri-
rá si dejamos de vacunar. El brote de sarampión que
crece en Europa (o en Estados Unidos, o Australia,
o…) no es sino el «te lo dije» que las matemáticas nos
están echando en cara. Y es que hemos demostrado
que la vacuna es solidaria y que gracias a ella, 93 es
igual a 100 (y… ¿en qué otras situaciones ganamos
siete así, por la cara?).
Referencias:
(
enlaces verificados a enero de 2019)
1 https://www.elespanol.com/mundo/
europa/20170623/225977935_0.html, también https://
www.redaccionmedica.com/secciones/sanidad-hoy/muere-
un-nino-por-sarampion-contagiado-por-sus-hermanos-sin-
vacunar-5093
2 https://www.elperiodico.com/es/sanidad/20180711/
muerte-marine-eraville-sarampion-francia-
antivacunas-6936401
3 Measles outbreak--California, December 2014 -
February 2015. Zipprich J, Winter K, Hacker J, et al.
https://www.cdc.gov/mmwr/preview/mmwrhtml/mm6406a5.
htm. MMWR Morb Mortal Wkly Rep. 2015;64:153–154.
4 https://ecdc.europa.eu/en/measles?bid=PvfemqWx
AAQYOzosPJvnsosDnuaebV_7PlQZ1XBTokM&items_
per_page=5&nid=20411&pager_type=infinite_scroll&sort_
by=title&sort_order=ASC&tid%5B0%5D%5Btarget_id%5D
=83&type%5B1439%5D=1439&page=2
5 Comité Vacunas –AEP, @CAV_AEP
6 Lucía, mi Pediatra, @luciapediatra, www.
luciamipediatra.com
7 Clara Grima Ruiz, Enrique Fernández Borja (2017)
Las Matemáticas vigilan tu salud: Modelos sobre
epidemias y vacunas
. El Café Cajal.
8 El País, junio 2017, «Javier Cárdenas propaga el bulo
de que las vacunas causan autismo», https://elpais.com/
elpais/2017/06/07/hechos/1496855559_006331.html
9 GOP Debate USA, September 2015, https://www.
washingtonpost.com/video/politics/carson-trump-paul-
debate-vaccines-and-autism/2015/09/17/1f117b78-
5d4c-11e5-8475-781cc9851652_video.html?utm_
term=.939d95530db1
10 Tom Huddleston Jr, Octubre 2015, “The Republican
debate completely smashed CNBC’s ratings record”,
http://fortune.com/2015/10/29/cnbc-gop-debate/
11 A.J.Wakefield et al., 1998, RETRACTED: “Ileal-
lymphoid-nodular hyperplasia, non-specific colitis, and
pervasive developmental disorder in children”,
The Lancet
,
Vol. 351, issue 9103, P637-641.
12 S.H.Murch et al, 2004, “Retraction of an
interpretation”,
The Lancet
, Vol. 363, issue 9411, P750.
13 Autism Speaks, 2015, “No MMR-Autism Link in
Large Study of Vaccinated vs. Unvaccinated Kids”, https://
www.autismspeaks.org/science-news/no-mmr-autism-link-
large-study-vaccinated-vs-unvaccinated-kids
14 https://www.latercera.com/que-pasa/noticia/
periodista-destapo-fraude-cientifico-intento-vincular-una-
vacuna-autismo/388605/
15 Artículo de Andrew Buncombe, mayo 2018,
“Trump claims vaccines and autism are liked but his own
experts vehemently disagree”,
The Independent
, https://
www.independent.co.uk/news/world/americas/trump-
vaccines-autism-links-anti-vaxxer-us-president-false-
vaccine-a8331836.html
16 A. Jain, J. Marshall, A. Buikema et al, 2015, “Autism
Occurrence by MMR Vaccine Status Among US Children
With Other Siblings With and Without Autism”,
JAMA
,
313(15), P1534-1540, https://jamanetwork.com/journals/
jama/fullarticle/2275444
17 Confederación Autismo España, http://www.autismo.
org.es/sobre-los-TEA/trastorno-del-especto-del-autismo
El brote de sarampión que crece en Europa (o en Estados
Unidos, o Australia, o…) no es sino el «te lo dije» que las
matemáticas nos están echando en cara.

el esc
é
ptico
59
Invierno 2018/19
y Autism Europe, http://www.autismeurope.org/about-
autism/prevalence-rate-of-autism/
18 Measles, Mumps and Rubella (MMR) Vaccination,
Centers for Disease Control and Prevention, https://www.
cdc.gov/vaccines/vpd/mmr/public/index.html
19 Spurious correlations, http://www.tylervigen.com/
spurious-correlations
.
Más en el libro de Tyler Vigen,
Spurious Correlations
, 2015, Hachette Books.
20 Véase, por ejemplo https://www.eldiario.es/
andalucia/NovusOrbis/delincuencia-inmigracion-
fenomenos-relacion_6_737086321.html, o también https://
www.larazon.es/historico/el-76-de-los-madrilenos-cree-
que-la-inmigracion-aumenta-la-delincuencia-PJLA_
RAZON_36419
21 «¿Han disparado los inmigrantes la delicuencia
en Alemania?» https://www.elconfidencial.com/
mundo/2018-08-29/alemania-inmigrantes-ultraderecha-
delincuencia_1609203/
22 https://www.factcheck.org/2018/06/is-
illegal-immigration-linked-to-more-or-less-crime/
o también, https://www.eldiario.es/andalucia/
NovusOrbis/delincuencia-inmigracion-fenomenos-
relacion_6_737086321.html
23 Autistic Self Advocacy Network, September 2015,
ASAN Statement on GOP Primary Debate Comments
on Autism and Vaccination, https://autisticadvocacy.
org/2015/09/asan-statement-on-gop-primary-debate-
comments-on-autism-and-vaccination/
24 P. Davies, S. Chapman, J. Leask, 2002,
“Antivaccination activists on the world wide web”,
Arch Dis
Child
; vol 87, 22-25
25 https://www.ncbi.nlm.nih.gov/pmc/articles/
PMC6122668/#REF38, sección Technology and its effects
on anti-vaccination movement
26 K. Lerman, X. Yan, X. Wu, (2015), “The
Majority Illusion in Social Networks”, https://arxiv.org/
abs/1506.03022
27 K. Schaul, October 2015, “Majority Illusion: a quick
puzzle to tell whether you know what people are thinking”,
Independent
, science section, https://www.independent.
co.uk/news/science/majority-illusion-a-quick-puzzle-to-tell-
whether-you-know-what-people-are-thinking-a6689636.
html
28 Cathy O’Neil, 2017,
Armas de destrucción
matemática: cómo el big data aumenta la desigualdad y
amenaza la democracia
(capítulo 1), Capitan Swing Libros
S.L
29 J. Gog, A. Conlan, “Life saving maths: How does
vaccination work?”
Motivate, maths enrichment for
schools
, University of Cambridge, https://motivate.maths.
org/content/MathsHealth/Vaccination/
30 https://es.wikipedia.org/wiki/Ritmo_
reproductivo_b%C3%A1sico
31 https://en.wikipedia.org/wiki/
Kermack%E2%80%93McKendrick_theory
32 Gráficos generados en http://www.public.asu.
edu/~hnesse/classes/sir.html?Alpha=2.14&Beta=0
.14&initialS=100000&initialI=1&initialR=0&iters=30
cambiando los parámetros de manera necesaria. https://
ibmathsresources.com/2014/05/17/modelling-infectious-
diseases/
33 F. Brauer, P. van den Driessche, J. Wu (Eds.),
2008,
Mathematical Epidemiology
, chapter 2, https://
www.springer.com/cda/content/document/cda_
downloaddocument/9783540789109-c1.pdf?SGWID=0-
0-45-532715-p173817706. O también https://mspace.
lib.umanitoba.ca/bitstream/handle/1993/32615/allotey_
clifford.pdf?sequence=1
Foto:Johnny Silvercloud, https://www.flickr.com/photos/johnnysilvercloud/32666033382/in/photolist-RLzXE7-Uka1NX/









